Trigonometric Identity: Connection to Circles

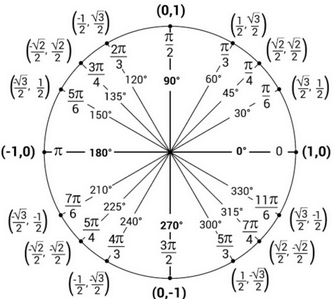
Trigonometric identities are intimately connected to the geometry of circles, especially when using the unit circle. In trigonometry, the unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane.

Meaning of Unit Circle

The term "unit circle" refers to a circle with a radius of exactly 1 unit. This circle is centered at the origin (0, 0) of a coordinate plane. The unit circle is a crucial concept in trigonometry because it simplifies the definitions of the trigonometric functions sine, cosine, and tangent. By using a circle with a radius of 1, the calculations and relationships between angles and coordinates become more straightforward.

Key Trigonometric Functions on the Unit Circle

For an angle θ in standard position (with the initial side on the positive x-axis), the coordinates of a point on the unit circle corresponding to θ are (cos(θ), sin(θ)).

In Summary

Trigonometric identities are essential for understanding the relationships between angles and sides in geometry, and they are deeply rooted in the properties of the unit circle.

For further understanding, here are some additional videos about the Trigonometric Identity of the Unit Circle.