Conclusion: The Evolution of Rational Functions
he rise of rational functions in mathematics can be attributed to the development of algebra, calculus, and their applications in solving real-world problems. Starting as simple ratios of polynomials, rational functions evolved with the advent of calculus, becoming central to the study of rates of change, optimization, and integration. The combined work of early mathematicians like Newton and Leibniz laid the groundwork for rational functions to flourish in mathematical theory and applications across various scientific disciplines. Henri Eugène Padé’s work further expanded their utility in approximation theory, and today, rational functions remain a foundational tool in both pure and applied mathematics, shaping our understanding of the world in ways that continue to impact modern science and technology.
Understanding Rational Functions in Calculus
Rational functions are an essential concept in calculus, where they play a significant role in many fundamental processes like differentiation, integration, and analyzing limits. Understanding how rational functions behave and how they can be manipulated helps in solving a wide range of calculus problems, from finding areas under curves to understanding the behavior of functions at specific points.
Rational functions are vital in calculus for several reasons. Here's how they are commonly used
Differentiation of Rational Functions
Calculating the derivative of a rational function (i.e., the rate of change of the function) often involves using the quotient rule. The quotient rule states that if you have a rational function of the form:

This rule is essential because it allows you to differentiate functions where the variables appear in both the numerator and the denominator, making the differentiation process more manageable.
2. Integration of Rational Functions
When integrating rational functions, the goal is often to express the function in a simpler form. Integration of rational functions is often performed through partial fraction decomposition, especially when the denominator can be factored. For example, to integrate a rational function like the picture shown in the right

where A and B are constants that are determined by solving a system of equations. After finding these constants, you can integrate each term separately, simplifying the problem.
Limits and Asymptotic Behavior
Rational functions are crucial in understanding limits and asymptotic behavior, which is essential for analyzing the behavior of functions as they approach certain points or infinity.
Horizontal Asymptotes: A rational function may approach a constant value as x → ∞ or x → -∞. This is known as a horizontal asymptote. (More on them later)
Vertical Asymptotes: These occur when the denominator approaches zero, causing the function to "blow up" (i.e., approach infinity or negative infinity). (More on them later)
Solving Real-World Problems
Rational functions model many real-world scenarios, and calculus allows us to solve optimization problems, analyze rates of change, and determine areas under curves. For instance:
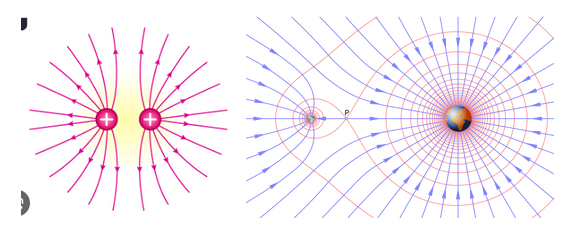
In physics, rational functions can represent systems where forces or fields are inversely proportional to distances or other variables (such as gravitational or electric fields).
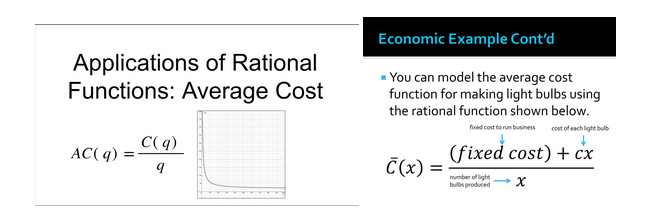
In economics, they may be used to model cost, revenue, or profit functions that involve ratios of polynomials.
For example, you might need to find the maximum or minimum of a rational function, which could be done by finding the critical points (where the derivative equals zero or is undefined) and using techniques like the first or second derivative test.
Conclusion
Rational functions play an integral role in calculus, offering powerful tools for differentiation, integration, and understanding limits. Through methods like the quotient rule, partial fraction decomposition, and limit analysis, rational functions help solve complex problems in both mathematics and the real world. By learning how to manipulate and analyze these functions, you gain a deeper understanding of the behavior of mathematical models and their practical applications in fields such as physics, engineering, and economics.
Solving rational functions according to calculus
How do we know if a problem is a rational function?
A function is considered a rational function if it can be expressed as the quotient (division) of two polynomials. More specifically, a rational function has the form:
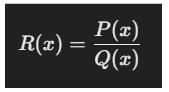
Where:
P(x) is the numerator polynomial.
Q(x) is the denominator polynomial.
Q(x) ≠ 0 (the denominator cannot be zero, as division by zero is undefined).
Steps to Identify a Rational Function
1.Check the Form of the Function:
If the function is a ratio of two expressions where both the numerator and the denominator are polynomials, it is a rational function.
2.Confirm Polynomial Structure:
Both the numerator P(x) and denominator Q(x) should have powers of x with non-negative integer exponents
Examples of polynomials are x^2 + 3x + 2, 5x^3 - x + 7,, or even constants like 4 (which is a polynomial with degree 0).
If either part of the expression (numerator or denominator) involves non-polynomial elements such as square roots, trigonometric functions, or logarithms, the function is not a rational function.
Check for Division
The function must involve division. If the function involves the multiplication or addition of polynomials like P(x) + Q(x), it is not a rational function.
Avoid Zero in the Denominator
For it to be a valid rational function, the denominator Q(x) must never be zero, because division by zero is undefined. Therefore, make sure the denominator doesn't introduce any undefined points.

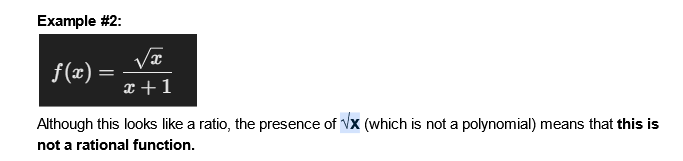








Summary of Examples
Rational Functions: They are always the ratio of two polynomials, where the numerator and denominator are algebraic expressions involving non-negative integer powers of x.
Non-Rational Functions: These include functions involving square roots, logarithms, trigonometric functions, or exponentials that are not polynomials.